20 CÂU HỎI
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Một công ty sản xuất và đưa ra bán trên thị trường sản phẩm \(A.\) Theo tính toán, khi đơn giá của mỗi sản phẩm \(A\) là \(x\) nghìn đồng thì doanh thu \(P\) (đơn vị nghìn đồng) là\(P\left( x \right) = - 560{x^2} + 50\,\,000x.\) Doanh thu tháng đầu tiên của công ty khi bán sản phẩm \(A\) với giá ưu đãi là 996 triệu đồng. Biết giá bán ưu đãi của sản phẩm \(A\) không vượt quá 50 nghìn đồng, hỏi giá ưu đãi của sản phẩm \(A\) mà công ty đã bán ở tháng đầu tiên là bao nhiêu?
A. \(32\,\,000\) đồng.
B. \(30\,\,000\) đồng.
C. \(300\,\,000\) đồng.
D. \(35\,\,000\) đồng.
Thời gian tự học (tính theo phút) trong một ngày của 40 học sinh lớp 9A được ghi lại trong bảng sau:
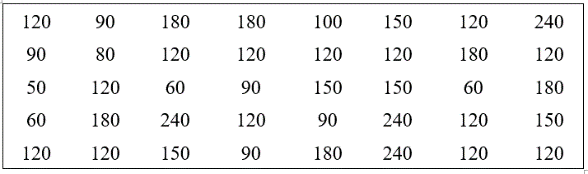
Tần số tương đối của học sinh có thời gian tự học 120 phút một ngày là
A. \(25\% .\)
B. \(20\% .\)
C. \(35\% .\)
D. \(50\% .\)
Cho hai đường tròn \(\left( {O;\,\,4{\rm{\;cm}}} \right)\) và \(\left( {I;\,\,5\,\,{\rm{cm}}} \right).\)Nếu \(OI = 1{\rm{\;cm}}\) thì hai đường tròn đã cho
A. tiếp xúc trong.
B. không giao nhau.
C. cắt nhau.
D. tiếp xúc ngoài.
Cặp số \(\left( {x;\,\,y} \right)\) nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 5\\2x + 3y = - 1\end{array} \right.?\)
A. \(\left( { - 1;\,\, - 1} \right).\)
B. \(\left( { - 1;\,\,1} \right).\)
C. \(\left( {1;\,\, - 1} \right).\)
D. \(\left( {1;\,\,1} \right).\)
Phương trình \(\left( {2m - 1} \right){x^2} + 4x + m - 1 = 0\) là phương trình bậc hai khi
A. \(m \ne 1.\)
B. \(m \ne 0.\)
C. \(m \ne \frac{1}{2}.\)
D. \(m = \frac{1}{2}.\)
Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AD\) (như hình vẽ). Biết \(\widehat {DAC} = 25^\circ .\) Số đo \(\widehat {ABC}\) bằng
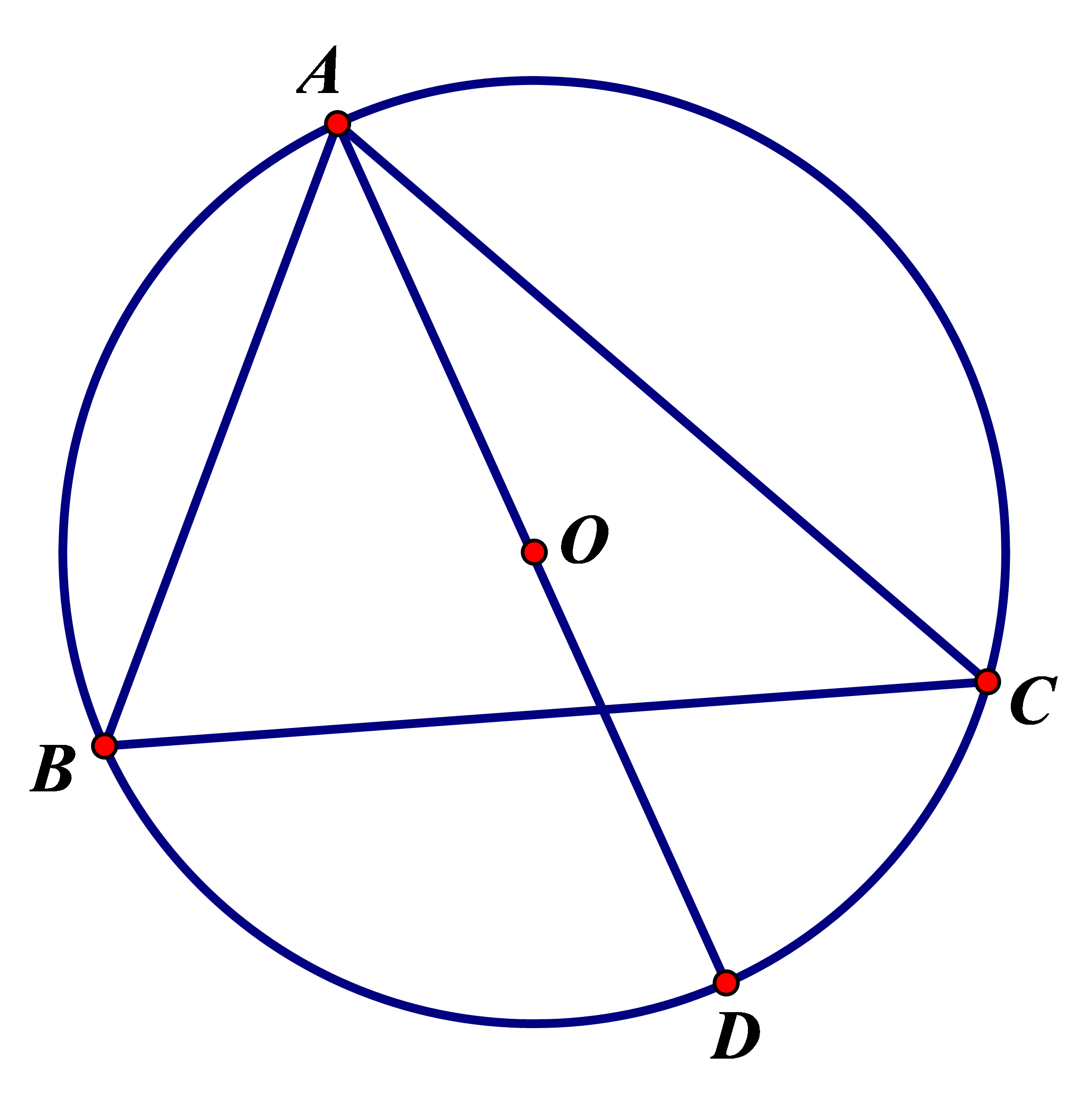
A. \(130^\circ .\)
B. \(90^\circ .\)
C. \(65^\circ .\)
D. \(50^\circ .\)
Một chiếc hộp chứa ba quả bóng có kích thước và khối lượng như nhau chỉ khác màu, trong đó có 1 quả bóng màu xanh, 1 quả bóng màu vàng và 1 quả bóng màu hồng. Lần lượt lấy ra ngẫu nhiên từng quả bóng từ trong hộp cho đến khi hộp hết bóng. Xác suất của biến cố ‘‘Quả bóng cuối cùng lấy ra có màu xanh’’ là
A. \(\frac{1}{6}.\)
B. \(\frac{2}{3}.\)
C. \(\frac{1}{3}.\)
D. \(\frac{1}{2}.\)
Biết \( - 8\) là một căn bậc hai của \(x.\) Căn bậc ba của \(x\) bằng
A. \( - 2.\)
B. \(4.\)
C. \(64.\)
D. \(2.\)
Lớp 9A có \(38\) học sinh tham gia buổi lao động trồng cây gây rừng. Biết cả lớp trồng được tất cả 170 cây xanh, trong đó mỗi bạn nữ trồng 4 cây, mỗi bạn nam trồng 5 cây. Nếu gọi số học sinh nam là \(x\) và số học sinh nữ là \(y\) thì \(x,\,\,y\) thoả mãn hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x + y = 38\\5x - 4y = 170\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x + y = 38\\5x + 4y = 170\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x + y = 38\\4x + 5y = 170\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x + y = 38\\4y - 5x = 170\end{array} \right..\)
Để trang trí lớp, bạn Lan đã dùng 4 miếng bìa hình quạt tròn cung \(120^\circ ,\) bán kính 30 cm (hình vẽ) để gấp trang trí. Tổng diện tích các miếng bìa bạn Lan đã dùng là
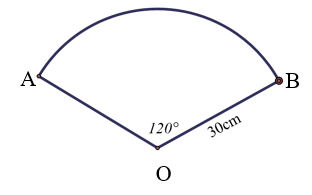
A. \(300\pi {\rm{\;c}}{{\rm{m}}^2}.\)
B. \(1200\pi {\rm{\;c}}{{\rm{m}}^2}.\)
C. \(1500\pi {\rm{\;c}}{{\rm{m}}^2}.\)
D. \(2400\pi {\rm{\;c}}{{\rm{m}}^2}.\)
Với \(a > 0,\,\,b < 0\) thì biểu thức \(A = \frac{{ - b}}{a}\sqrt {\frac{{{a^3}}}{{{b^2}}}} \) bằng
A. \(\sqrt a .\)
B. \(\frac{a}{b}\sqrt a .\)
C. \( - \sqrt a .\)
D. \( - \frac{a}{b}\sqrt a .\)
Tất cả các giá trị của biến \(x\) để biểu thức \(\sqrt {4x - 2} \) có nghĩa là
A. \(x \ge 0.\)
B. \(x \ge - 2.\)
C. \(x \ge \frac{{ - 1}}{2}.\)
D. \(x \ge \frac{1}{2}.\)
Nam muốn mua một chiếc xe đạp có giá 3200000 đồng. Hiện tại, Nam đã có \[1\,\,200\,\,000\] đồng. Nam dự định mỗi tháng sẽ tiết kiệm một số tiền cố định như nhau từ tiền ăn sáng và tiền tiêu vặt mà bố mẹ cho để mua xe. Hỏi Nam cần tiết kiệm ít nhất bao nhiêu tiền mỗi tháng để sau 8 tháng có đủ tiền mua xe?
A. \(200\,\,000\) đồng.
B. \(250\,\,000\) đồng.
C. \(300\,\,000\) đồng.
D. \(25\,\,000\) đồng.
Tính độ dài đường tròn ngoại tiếp tam giác \(ABC\) vuông tại \(A\) có \(AB = 6{\rm{\;cm}},\,\,AC = 8{\rm{\;cm}}.\)
A. \(40\pi {\rm{\;cm}}.\)
B. \(5\pi {\rm{\;cm}}.\)
C. \(10\pi {\rm{\;cm}}.\)
D. \(20\pi {\rm{\;cm}}.\)
Hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\)có đồ thị nằm phía trên trục hoành khi
A. \(m > 1.\)
B. \(m > - 1.\)
C. \(m < - 1.\)
D. \(m < 1.\)
Chọn ngẫu nhiên một số có hai chữ số. Xác suất để số được chọn là số chính phương (là số bằng bình phương đúng của một số nguyên) bằng bao nhiêu?
A. \(\frac{2}{{45}}.\)
B. \(\frac{1}{{15}}.\)
C. \(\frac{7}{{90}}.\)
D. \(\frac{1}{{10}}.\)
Cho tam giác \(MNP\) vuông tại \(M.\) Trong các khẳng định sau khẳng định nào đúng?
A. \(\sin N = \cos \left( {90^\circ - P} \right).\)
B. \(\tan M = \cot P.\)
C. \(\tan N \cdot \cot P = 1.\)
D. \(\sin N = \cos P.\)
Nếu đặt một chiếc thang dài 4m cách chân tường 2m (hình vẽ) thì góc tạo bởi thang và mặt đất bằng
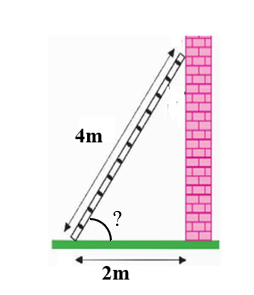
A. \(30^\circ .\)
B. \(60^\circ .\)
C. \(90^\circ .\)
D. \(50^\circ .\)
Biết hệ phương trình \(\left\{ \begin{array}{l}x - my = 2\\nx + y = 3\end{array} \right.\) có nghiệm \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\) Khi đó giá trị của biểu thức \(2\,\,025m + {n^{2\,\,025}}\) bằng
A. \(2\,\,025.\)
B. \(1.\)
C. \(2\,\,026.\)
D. \(0.\)
Gieo ngẫu nhiên hai con xúc xắc cân đối đồng chất. Xác suất của biến cố A: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8” là
A. \(\frac{5}{{36}}.\)
B. \(\frac{1}{6}.\)
C. \(\frac{1}{9}.\)
D. \(\frac{1}{{12}}.\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải