50 CÂU HỎI
Cho số phức . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức liên hợp của số phức z?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có và . Tìm tọa độ trọng tâm G của tam giác ABC
A.
B.
C.
D.
Có 16 đội bóng tham gia thi đấu. Hỏi cần phải tổ chức bao nhiêu trận đấu sao cho hai đội bất kì đều gặp nhau đúng một lần?
A. 8
B. 16
C. 120
D. 240
Người ta đặt một khối chóp tứ giác đều lên trên một khối lập phương để thu được một khối mới như trong hình. Tính thể tích V của khối mới thu được?
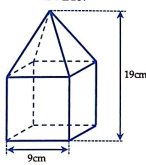
A. V=513 (cm3)
B. V=999 (cm3)
C. V=1242 (cm3)
D. V=1539 (cm3)
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với và . Mệnh đề nào dưới đây sai?
A.
B.
C.
D.
Cho đồ thị hàm số y=f(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.

A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a. Tính góc giữa đường thẳng SB và mặt phẳng (SAC).
A. 30°
B. 45°
C. 60°
D. 90°
Cho hàm số y=f(x) xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:

Tìm tất cả các giá trị của tham số thực m để phương trình f(x)-m=0 có nghiệm duy nhất.
A.
B.
C.
D.
Tìm giá trị lớn nhất của hàm số trên đoạn .
A.
B.
C.
D.
Cho tam giác ABC đều cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh S của hính nón
A.
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
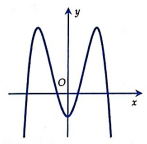
A.
B.
C.
D.
Có bao nhiêu số nguyên dương x thỏa mãn điều kiện ?
A. 19
B. 18
C. 21
D. 20
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng . Viết phương trình mặt phẳng đi qua A và song song với mặt phẳng .
A.
B.
C.
D.
Cho phương trình có các nghiệm là . Tính giá trị biểu thức .
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA=a. Tính theo a khoảng cách d giữa hai đường thẳng SC và BD.
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và . Gọi M là điểm trên mặt phẳng (Oxz) sao cho t ổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ của điểm M.
A.
B.
C.
D.
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x () là một hình chữ nhật có hai kích thước là x và .
A.
B.
C.
D.
Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây. Đó là hàm số nào?
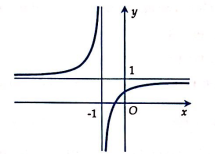
A.
B.
C.
D.
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn là hữu hạn
A.
B.
C.
D.
Một đa giác đều có 54 đường chéo. Tính số hình chữ nhật có 4 đỉnh là 4 đỉnh của đa giác đều đó.
A. 702
B. 351
C. 30
D. 15
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng , mặt phẳng và điểm . Viết phương trình đường thẳng cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN.
A.
B.
C.
D.
Cho số tự nhiên x thỏa mãn . Tìm số khác ước tự nhiên của x.
A. 8
B. 9
C. 10
D. 11
Từ các chữ số 1, 2, 3, 4, 5, 6 lập các số tự nhiên gồm 6 chữ số đôi một khác nhau. Hỏi trong số đó có bao nhiêu số nhỏ hơn 432000?
A. 414
B. 360
C. 408
D. 420
Sau một trận mưa, cứ một mét vuông mặt đất thì hứng một lít rưỡi nước mưa rơi xuống. Hỏi mực nước trong một bể bơi ngoài trời tăng lên bao nhiêu sau trận mưa?
A. Phụ thuộc vào kích thước của bể bơi
B. 0,015 (cm)
C. 0,15 (cm)
D. 1,5 (cm)
Cho số phức ; thỏa mãn . Tìm giá trị của biểu thức .
A.
B.
C.
D.
Cho hai số thực a và b (a<b) sao cho đạt giá trị lớn nhất. Tìm b-a.
A. 2
B. 4
C. 6
D. 8
Cho hình lăng trụ tam giác đều có và . Gọi M và N lần lượt là trung điểm của và . Tính cosin của góc tạo bởi hai mặt phẳng và (BCMN).
A.
B.
C.
D.
Cho hàm số . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị () thỏa mãn .
A.
B. ‒1
C.
D. 5
Tìm số điểm cực trị của hàm số .
A. n=4
B. n=2
C. n=3
D. n=1
Gọi n là tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . Tìm n.
A. n=4
B. n=2
C. n=3
D. n=1
Cho phương trình . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình có bốn nghiệm phân biệt. Mệnh đề nào dưới đây đúng?
A. S là một khoảng
B. S là một đoạn
C. S là hợp của hai đoạn rời nhau
D. S là hợp của hai khoảng rời nhau
Gọi (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.
A. 40,8 cm
B. 38,4 cm
C. 36 cm
D. 51,2 cm
Trong không gian với hệ tọa độ Oxyz, cho điểm . Viết phương trình mặt phẳng (P) đi qua H, cắt các trục lần lượt tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC.
A.
B.
C.
D.
Cho ba đường cong a, b, c như hình bên. Đồ thị của các hàm số lần lượt là
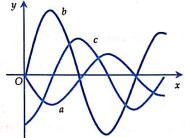
A. a,b,c
B. b,a,c
C. b,c,a
D. c,b,a
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên khoảng .
A.
B.
C.
D.
Cho hàm số . Hỏi có bao nhiêu giá trị nguyên dương của hàm số m để hàm số có hai điểm cực trị () thỏa mãn .
A. 2
B. 1
C. 0
D. vô số
Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các viên bi đều tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với 6 viên bi xung quanh và mỗi viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Tính diện tích đáy S của cái lọ.
A.
B.
C.
D.
Một bồn nước inox được thiết kế có dạng hình trụ (có nắp) đựng được 10 mét khối nước. Tìm bán kính r của đáy bồn nước biết lượng inox được sử dụng để làm bồn nước là ít nhất?
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng , cạnh SC vuông góc với đáy và SC=1. Gọi D và E lần lượt là trung điểm của AB và BC. Tính góc giữa hai đường thẳng CD và SE.
A.
B.
C.
D.
Biết , theo thứ tự lập thành một cấp số cộng và x là một số tự nhiên. Tìm tổng các chữ số của x.
A. 8
B. 9
C. 10
D. 11
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình =m có đúng hai nghiệm thuộc đoạn . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Cho hình lập phương có cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng và .
A.
B.
C.
D.
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 5 điểm cực trị.

A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và điểm?(2;2;0).. Viết phương trình mặt phẳng (OAB), biết rằng điểm B thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.
A. ?−?−2?=0
B.
C.
D.
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên. Đặt . Tìm số nghiệm của phương trình .

A. 2
B. 4
C. 6
D. 8
Cho hàm số có đồ thị là (C). Gọi T là tập hợp tất cả các điểm thuộc đường thẳng y=x-1 mà từ điểm đó kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tìm tổng tung độ của các điểm thuộc T.
A. ‒1
B. 0
C. 1
D. 2
Để cấp tiền cho con trai tên là Lâm học đại học, ông Anh gửi vào ngân hàng 200 triệu đồng với lãi suất cố định 0,7%/ tháng, số tiền lãi hàng tháng được nhập vào vốn để tính lãi cho tháng tiếp theo (thể thức lãi kép). Cuối mỗi tháng, sau khi chốt lãi, ngân hàng sẽ chuyển vào tài khoản của Lâm một khoản tiền giống nhau. Tính số tiền m mỗi tháng Lâm nhận được từ ngân hàng, biết rằng sau bốn năm (48 tháng), Lâm nhận hết số tiền cả vốn lẫn lãi mà ông Anh đã gửi vào ngân hàng (kết quả làm tròn đến đồng).
A. (đồng)
B. (đồng)
C. (đồng)
D. (đồng)
Cho hai số phức và . Gọi là số phức thỏa mãn . Tìm a+b, biết biểu thức đạt giá trị nhỏ nhất.
A. ‒3
B. ‒7
C. 3
D. 7
Có 8 người ngồi xung quanh một chiếc bàn tròn. Mỗi người cầm một đồng xu cân đối, đồng chất. Cả 8 người đồng thời tung đồng xu. Ai tung được mặt ngửa thì phải đứng dậy, ai tung được mặt sấp thì ngồi yên tại chỗ. Tính xác suất sao cho không có hai người nào ngồi cạnh nhau phải đứng dậy?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ đứng có , , và , trong đó là các số thực dương và thỏa mãn . Khi khoảng cách giữa hai đường thẳng và lớn nhất thì mặt cầu ngoại tiếp hình lăng trụ có bán kính R bằng bao nhiêu?
A.
B.
C.
D.


