31 CÂU HỎI
Tìm điểm M biểu diễn số phức
A. M(1;-2)
B. M(2;-1)
C. M(-2;1)
D. M(2;1)
Trên mặt phẳng tọa độ, điểm M là điểm biểu diển của số phức z (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diển của số phức 2z?
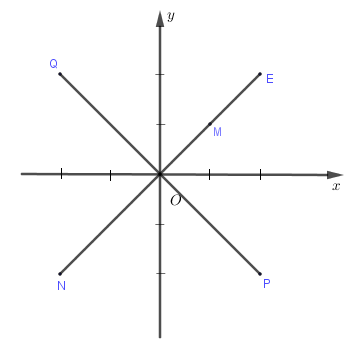
A. Điểm N.
B. Điểm Q.
C. Điểm E.
D. Điểm P.
Gọi A là điểm biểu diễn của số phức ]z=-1+6i và B là điểm biểu diễn của số phức z'=-1-6i. Mệnh đề nào sau đây là đúng?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
Gọi M và N lần lượt là điểm biểu diễn của các số phức khác 0. Khi đó khẳng định nào sau đây sai?
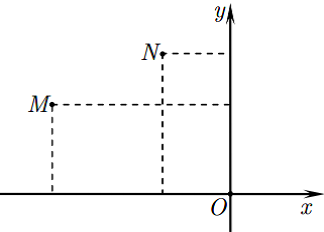
A.
B.
C.
D.
Số phức z được biểu diễn trên trên mặt phẳng như hình vẽ.
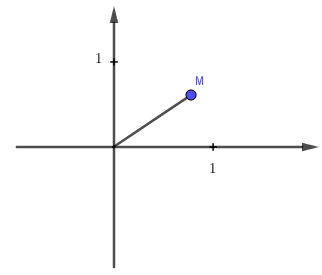
Hỏi hình nào biểu diễn cho số phức
A. 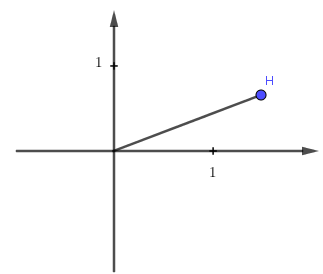
B. 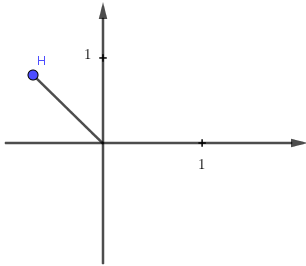
C. 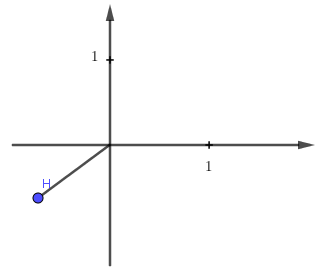
D. 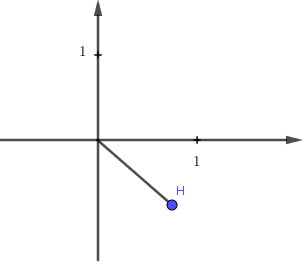
Cho số phức z thỏa mãn (1+i)z=3-i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình bên ?
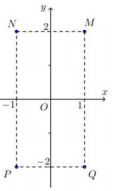
A. Điểm P
B. Điểm Q
C. Điểm M
D. Điểm N
Cho số phức z thỏa mãn (2-i)z=7-i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình dưới.
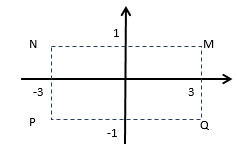
A. Điểm P
B. Điểm Q
C. Điểm M
D. Điểm N
Cho số phức . Tìm số phức
A. w=7-3i
B. w=-3-3i
C. w=3+7i
D. w=-7-7i
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M,N,P,Q. Khi đó điểm biểu diễn của số phức w là
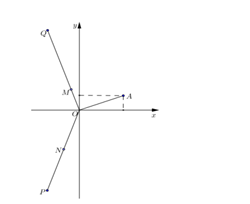
A. Điểm Q
B. Điểm M
C. Điểm N
D. Điểm P
Số phức z thỏa mãn . Khi đó:
A. z là số thuần ảo
B. Môđun của z bằng 1
C. z là số thực nhỏ hơn hoặc bằng 0
D. Phần thực của z là số âm
Trong mặt phẳng phức gọi A,B,C lần lượt là các điểm biểu diễn của các số phức . Khẳng định nào sau đây là sai?
A. B và C đối xứng với nhau qua trục tung.
B. Trọng tâm của tam giác ABC là G(1;23).
C. A và B đối xứng với nhau qua trục hoành.
D. A,B,C nằm trên đường tròn tâm tại gốc tọa độ và bán kính bằng .
Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên dưới. Modun của z bằng:
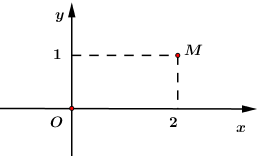
A. 5
B.
C.
D. 3
Gọi A và B lần lượt là điểm biểu diễn của số phức và Trung điểm của đoạn thẳng AB có tọa độ là:
A. (1;-3)
B. (2;3)
C. (2;1)
D. (4;2)
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn là:
A. một đường thẳng.
B. một đường tròn.
C. một elip.
D. một điểm.
Cho các số phức có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng
A. 8
B. 2
C. 4
D. 6
Cho hai số phức . Trong mặt phẳng tọa độ, điểm biểu diễn cho số phức là:
A. P(7;−1)
B. Q(5;−1)
C. M(7;0)
D. N(5;0)
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện và là số thuần ảo?
A. 2
B. 3
C. 4
D. 0
Cho ba điểm A,B,C lần lượt biểu diễn các số phức sau . Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.
A. m = -3
B. m = 1
C. m = -1
D. m = 3
Tập điểm biểu diễn số phức z thỏa mãn là:
A. Cả mặt phẳng
B. Đường thẳng
C. Một điểm
D. Hai đường thẳng
Cho các số phức z thỏa mãn |z+1+i| = |z-1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3=0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Cho số phức z thỏa mãn là số thực. Tập hợp điểm MM biểu diễn số phức z là:
A. Đường tròn
B. Đường thẳng
C. Hai đường thẳng
D. Một điểm duy nhất
Cho số phức z thay đổi, luôn có |z|=2. Khi đó tập hợp điểm biểu diễn số phức là
A. Đường tròn
B. Đường tròn
C. Đường tròn
D. Đường tròn
Cho các số phức z thỏa mãn |z|=4. Biết rằng tập hợp các điểm biểu diễn số phức w=(3+4i)z+i là một đường tròn. Tính bán kính r của đường tròn đó.
A. r = 4
B. r = 5
C. r = 20
D. r = 22
Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện là hình gì?
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường Elip.
D. Một đường tròn.
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện
A. Đường tròn
B. Elip
C. Đường tròn
D. Elip
Cho số phức với . Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng
A.
B.
C. 1
D.
Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức z=-1+2i và là góc lượng giác có tia đầu Ox, tia cuối OM. Tính
A.
B. -1
C.
D.
Cho các số phức và có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:
A.
B. 12
C.
D. 9
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức . Gọi S diện tích tứ giác ABCD. Tính S.
A.
B.
C.
D.
Cho các số phức z thỏa mãn |z|=2 và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức là một trong bốn điểm M, N, P, Q
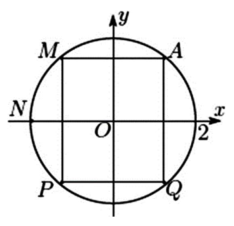 Khi đó điểm biểu diễn của số phức w là
Khi đó điểm biểu diễn của số phức w là
A. Điểm N
B. Điểm Q
C. Điểm P
D. Điểm M
Cho hai số phức thỏa mãn . Gọi M,N lần lượt là các điểm biểu diễn của số phức và số phức . Biết . Tính
A.
B.
C.
D.

