42 CÂU HỎI
Cho biết GTLN của hàm số f(x) trên là M = −2. Chọn khẳng định đúng:
A.
B.
C.
D.
Cho hàm số f(x) xác định trên và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên đoạn là :
A.−1
B.1
C.π
D.0
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn lần lượt là
A.
B.
C.
D.
Gọi m là giá trị nhỏ nhất của hàm số trên khoảng . Tìm m?
A.
B.
C.
D.
Cho hàm số có bảng biến thiên như hình vẽ, chọn kết luận đúng:
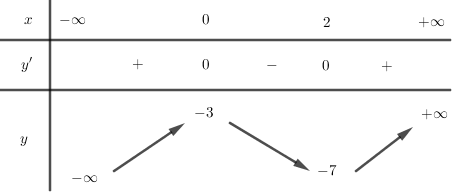
A.
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
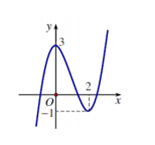
A.
B. Hàm số đồng biến trên khoảng
C. Giá trị cực tiểu của hàm số bằng 2
D.
Cho hàm số có bảng biến thiên như sau:
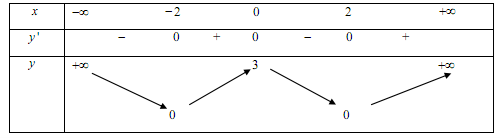
Khẳng định nào sau đây là khẳng định đúng?
A.Hàm số đạt cực đại tại x = 3
B.GTNN của hàm số bằng giá trị cực tiểu của hàm số.
C.Hàm số không có GTNN.
D.Hàm số có GTLN là 3.
Cho hàm số xác định và liên tục trên , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số trên đoạn
A.
B.
C.
D.
Gọi M,N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tính .
A.
B.
C. 3
D.
Hàm số nào dưới đây có giá trị nhỏ nhất trên tập xác định?
A.
B.
C.
D.
Đề thi THPT QG - 2021 - mã 101
Trên đoạn hàm số đạt giá trị lớn nhất tại điểm
A.
B.
C.
D.
Cho hàm số f(x) có bảng biến thiên như hình vẽ:
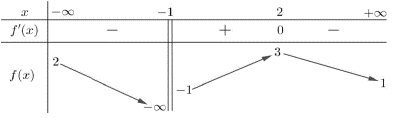
Tìm điều kiện của tham số mm để với mọi
A.
B.
C.
D.
Tìm giá trị lớn nhất của hàm số trên đoạn
A.M = −10
B.M = −7
C.M = −5
D.M = 1
Tìm GTLN và GTNN của hàm số trên đoạn
A.
B.
C.
D.
Giá trị lớn nhất của hàm số trên tập xác định của nó là:
A. -2
B.
C. 8
D. 10
Gọi giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn lần lượt là M và m. Khi đó giá trị của M.m là:
A.−2
B.46
C.−23
D.23
Cho hàm số Giá trị nhỏ nhất của hàm số trên khoảng là:
A.2
B.−3
C.5
D.10
Cho hàm số . Giá trị lớn nhất của hàm số trên bằng khi m bằng:
A.−5
B.0
C.5
D.
Cho hàm số , giá trị nhỏ nhất của hàm số trên bằng 2 khi:
A.
B.
C.
D.
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình dưới. Gọi a,A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của f(x+1) trên đoạn Giá trị bằng:
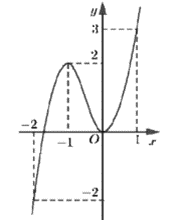
A.−1
B.2
C.0
D.3
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ
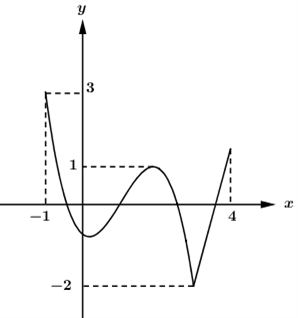
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn để bất phương trình đúng với mọi x thuộc đoạn
A.6
B.5
C.7
D.8
Một sợi dây kim loại dài a(cm) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài x(cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
A.
B.
C.
D.
Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Khi đó, giá trị của tổng bằng:
A.
B.
C.
D.
Cho hàm số liên tục trên có đồ thị như hình vẽ. Đặt . Khi đó giá trị lớn nhất của hàm số g(x) trên đoạn là:
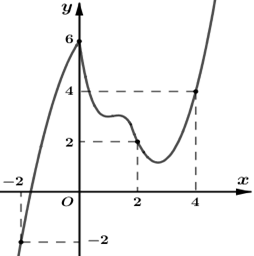
A.g(−2).
B.g(2).
C.g(4).
D.g(0).
Cho hàm số có đạo hàm trên và có đồ thị như hình vẽ bên. Xét hàm số . Giá trị của tham số m để giá trị lớn nhất của hàm số g(x) trên đoạn bằng 9 là:
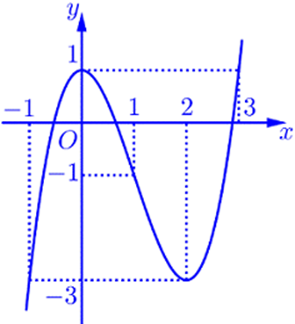
A.m=10
B.m=6
C.m=12
D.m=8
Cho hàm số liên tục trên R và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên Giá trị của M + m bằng
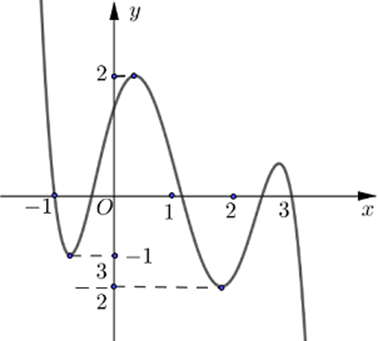
A.
B.
C. 2
D. 1
Có bao nhiêu số nguyên để
A.6
B.4
C.3
D.5
Cho hai số thực x,y thỏa mãn . Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức Có bao nhiêu giá trị nguyên thuộc đoạn của tham số aa để ?
A.17.
B.16.
C.15.
D.18.
Cho f(x) mà đồ thị hàm số như hình vẽ bên
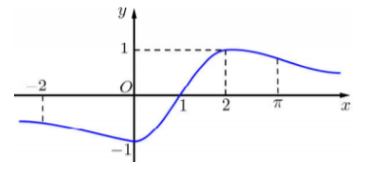
Bất phương trình nghiệm đúng với mọi khi và chỉ khi:
A.
B.
C.
D.
Cho Gọi Khi đó M − m bằng:
A. 1
B.
C.
D.
Cho hàm số f(x). Biết hàm số f′(x) có đồ thị như hình dưới đây. Trên đoạn hàm số đạt giá trị nhỏ nhất tại điểm 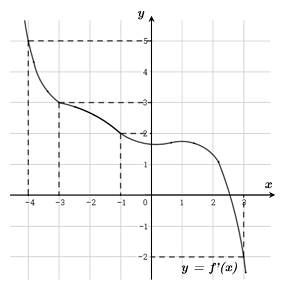
A.x = −1.
B.x = −4.
C.x = −3.
D.x = 3.
Cho hàm số . Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số có giá trị nhỏ nhất trên khoảng
A.2
B.1
C.Vô số
D.3
Cho x,y là các số thực thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức .
A. 1
B.
C.
D. 0
Cho các số thực x,y thay đổi thỏa mãn và hàm số . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của Tính M+m?
A.
B.
C.
D.
Cho hàm số có đồ thị là (C). Gọi là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất,
tính tổng .
A. 1
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ. Xét hàm số . Mệnh đề nào dưới đây đúng?
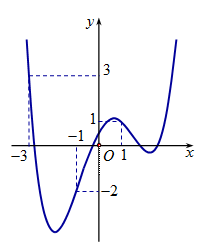
A.
B.
C.
D.
Hàm số (tham số m;n) đồng biến trên khoảng . Giá trị nhỏ nhất của biểu thức bằng
A. -16
B. 4
C.
D.
Nhà xe khoán cho hai tài xế ta-xi An và Bình mỗi người lần lượt nhận 32 lít và 72 lít xăng. Hỏi tổng số ngày ít nhất là bao nhiêu để hai tài xế chạy tiêu thụ hết số xăng của mình được khoán, biết rằng chỉ tiêu cho hai người một ngày tổng cộng chỉ chạy đủ hết 10 lít xăng?
A.20 ngày.
B.15 ngày.
C.10 ngày
D.25 ngày
Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo C (như hình vẽ bên). Biết rằng chi phí đi đường thủy là 5 USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
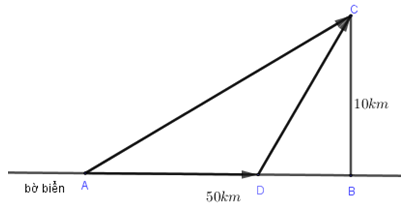
A.
B.
C. 50 km
D.
Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được nước. Biết tỉ lệ giữa chiều cao và chiều rộng của bể bằng 3. Xác định diện tích đáy của bể cá để tiết kiệm nguyên vật liệu nhất.
A.
B.
C.
D.
Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê. Mỗi một căn hộ không thuê nữa (bỏ trống) thì công ty lại phải tăng số tiền thuê của những căn hộ còn lại thêm 50.000 đồng. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
A.115.250.000 đồng
B.101.250.000 đồng
C.100.000.000 đồng
D.100.250.000 đồng

